Log-log graphs scale both axes logarithmically, which causes functions of the form f(x) = a · xk to be depicted as straight lines with slope equal to the exponent k.
Expressed mathematically, x is the logarithm of n to the base b if bx = n, in which case one writes x = log b n. For example, 2 3 = 8; therefore, 3 is the logarithm of 8 to base 2, or 3 = log 2 8.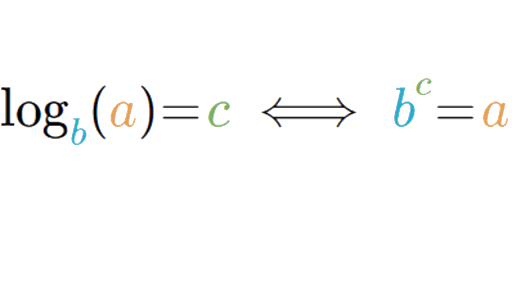
For example the result for 2 x = 5 can be given as a logarithm, x = log 2 (5) . You will learn how to evaluate this logarithmic expression over the following lessons.